AI For Trading: Exercise:finding pairs (29)

Checking if a pair of stocks is cointegrated

Imports

import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from statsmodels.tsa.stattools import adfuller
import matplotlib.pyplot as plt
import quiz_tests

/opt/conda/lib/python3.6/site-packages/statsmodels/compat/pandas.py:56: FutureWarning: The pandas.core.datetools module is deprecated and will be removed in a future version. Please use the pandas.tseries module instead.
  from pandas.core import datetools

# Set plotting options
%matplotlib inline
plt.rc('figure', figsize=(16, 9))

# just set the seed for the random number generator
np.random.seed(2018)
# use returns to create a price series
drift = 100

# 高斯分布的概率密度函数(获取1000个数据)
r1 = np.random.normal(0, 1, 1000) 
# print(r1)

# print(np.cumsum(r1))

s1 = pd.Series(np.cumsum(r1), name='s1') + drift
s1.plot(figsize=(14,6))
plt.show()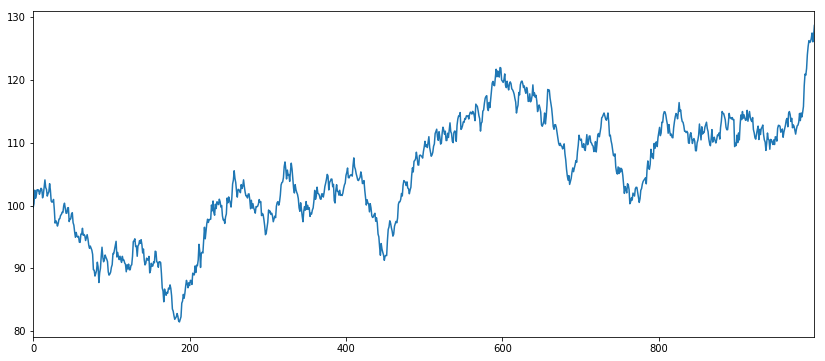

offset = 10
noise = np.random.normal(0, 1, 1000)
s2 = s1 + offset + noise
s2.name = 's2'
pd.concat([s1, s2], axis=1).plot(figsize=(15,6))
plt.show()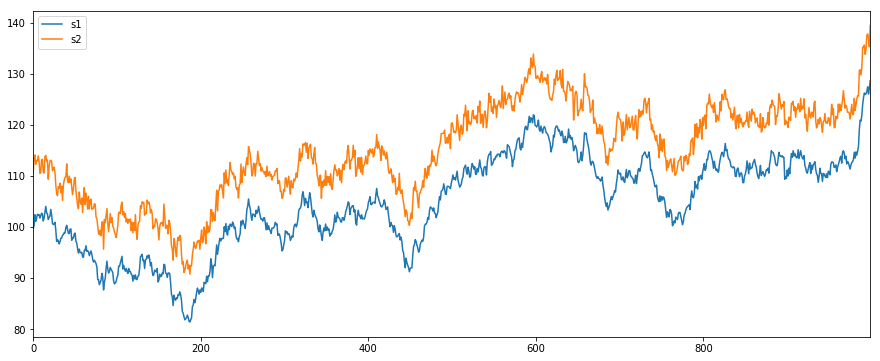

price_ratio = s2/s1
price_ratio.plot(figsize=(15,7)) 
plt.axhline(price_ratio.mean(), color='black') 
plt.xlabel('Days')
plt.legend(['s2/s1 price ratio', 'average price ratio'])
plt.show()
print(f"average price ratio {price_ratio.mean():.4f}")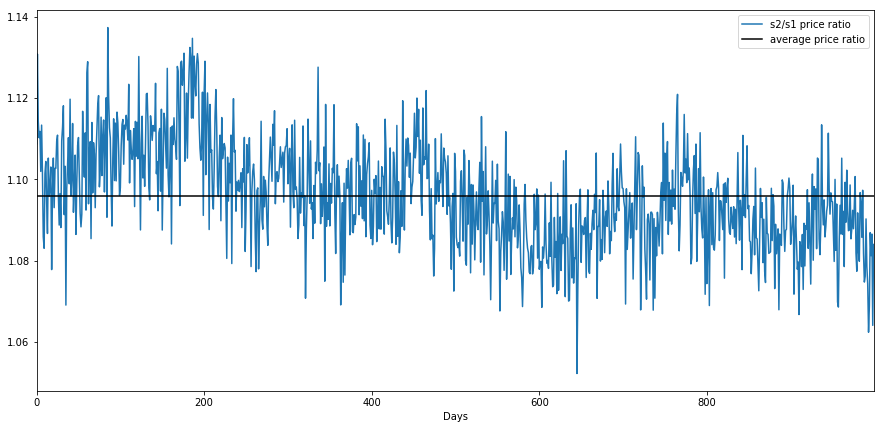

average price ratio 1.0960

Calculate hedge ratio with regression

Linear Regression

Note that the LinearRegression().fit() expects 2D numpy arrays. Since s1 and s2 are pandas series, we can use Series.values to get the values as a numpy array. Since these are 1D arrays, we can use numpy.reshape(-1,1) to make these 1000 row by 1 column 2 dimensional arrays

type(s1)

pandas.core.series.Series

type(s1.values)

numpy.ndarray

s1.values.reshape(-1,1).shape

(1000, 1)

lr = LinearRegression()
lr.fit(s1.values.reshape(-1,1),s2.values.reshape(-1,1))

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)

hedge_ratio = lr.coef_[0][0]
hedge_ratio

1.002234357791276

intercept = lr.intercept_[0]
intercept

9.753022747192901

print(f"hedge ratio from regression is {hedge_ratio:.4f}, intercept is {intercept:.4f}")

hedge ratio from regression is 1.0022, intercept is 9.7530

Question

Do you think we'll need the intercept when calculating the spread? Why or why not?

Calculate the spread

spread = s2 - s1 * hedge_ratio

print(f"Average spread is {spread.mean()}")

Average spread is 9.753022747192906

spread.plot(figsize=(15,7)) 
plt.axhline(spread.mean(), color='black') 
plt.xlabel('Days')
plt.legend(['Spread: s2 - hedge_ratio * s1', 'average spread'])
plt.show()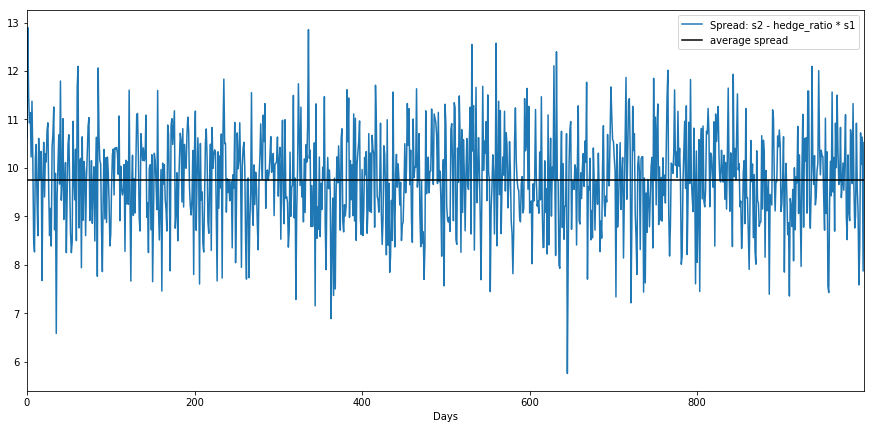

Let's see what we get if we include the intercept of the regression

spread_with_intercept = s2 - (s1 * hedge_ratio + intercept)
print(f"Average spread with intercept included is {spread_with_intercept.mean()}")

Average spread with intercept included is 6.210143510543276e-15

spread_with_intercept.plot(figsize=(15,7)) 
plt.axhline(spread_with_intercept.mean(), color='black') 
plt.xlabel('Days')
plt.legend(['Spread: s2 - (hedge_ratio * s1 + intercept)', 'average spread'])
plt.show()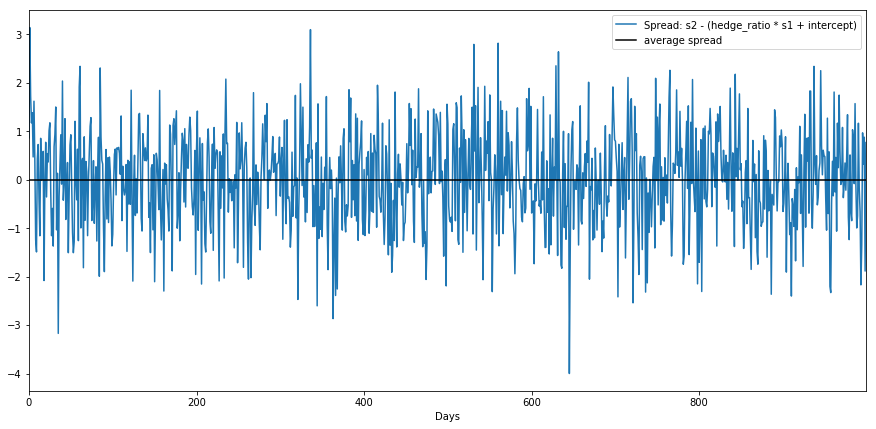

Quiz

Check if spread is stationary using Augmented Dickey Fuller Test

The adfuller function is part of the statsmodel library.

adfuller(x, maxlag=None, regression='c', autolag='AIC', store=False, regresults=False)[source]

adf (float) – Test statistic
pvalue (float) – p-value
...

def is_spread_stationary(spread, p_level=0.05):
    """
    spread: obtained from linear combination of two series with a hedge ratio

    p_level: level of significance required to reject null hypothesis of non-stationarity

    returns:
        True if spread can be considered stationary
        False otherwise
    """
    #TODO: use the adfuller function to check the spread
    adf_result = adfuller(spread)

    #get the p-value
    pvalue = adf_result[1]

    print(f"pvalue {pvalue:.4f}")
    if pvalue <= p_level:
        print(f"pvalue is <= {p_level}, assume spread is stationary")
        return True
    else:
        print(f"pvalue is > {p_level}, assume spread is not stationary")
        return False

quiz_tests.test_is_spread_stationary(is_spread_stationary)

pvalue 0.0000
pvalue is <= 0.05, assume spread is stationary
Tests Passed

# Try out your function
print(f"Are the two series candidates for pairs trading? {is_spread_stationary(spread)}")

pvalue 0.0000
pvalue is <= 0.05, assume spread is stationary
Are the two series candidates for pairs trading? True

为者常成，行者常至