Python:线性代数-向量-大小和方向及场中的运算 (四十三)

大小和方向

每个向量都包含运动的大小和方向。
我们来计算下向量 \(\vec{x}=\begin{bmatrix} 4 \\2 \end{bmatrix} \) 的大小和方向。
大小的符号是 || ||。

要计算二维向量的大小，我们将使用勾股定理
在示例中，向量大小的计算方式如下所示：
$$ ||\vec{x}|| = \sqrt{4^2 + 2^2}$$

其中 4 是向量的水平分量，2 是向量的垂直分量。

要计算运动方向，我们将使用夹角。我们可以用度数或弧度来表示。在此示例中，我们将采用度数（我们始终可以将度数转换为弧度，反之亦然）。

我们再次看看向量 \(\vec{x}\) 。它与水平轴的夹角为 \(\theta\)。

请看下图：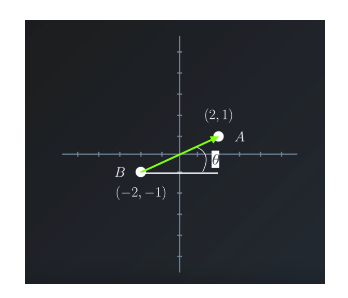

要计算 \(\theta\)，我们将运用三角学知识！

对于下图中表示的夹角\(\theta\)，计算方式如下所示：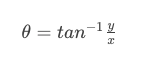

方程 3

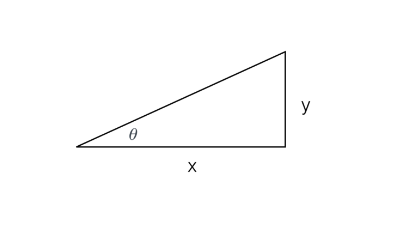
因此，在我们的示例中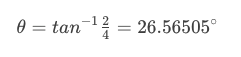

详细了解二维向量的大小和方向，请访问以下链接。

场中的运算

实数域 \(\mathbb{R^n}\)中的运算
与任何场一样，我们可以定义实数域 \(\mathbb{R^n}\)的数学运算。

这些运算包括：

• 加法
• 乘法
  我们还需要定义域中的元素 0 和 1。

上述运算遵守实数域公理：

• 结合律
• 交换律
• 分配律
• 单元性（定义加上零和乘以一）
• 逆元（定义加减逆元和乘除逆元）

在这节课，我们将重点讲解向量加法和标量与向量乘法。

为者常成，行者常至