Python:线性代数-向量-线性组合 (四十四)

线性组合、张成和基本向量

单位向量：长度为1向右或向上的向量为标向量

标量经过缩放处理的向量的和，将两个经过缩放处理的向量相加的思路十分重要。
向量\(\vec{i}\)和\(\vec{j}\)称为坐标系的基。

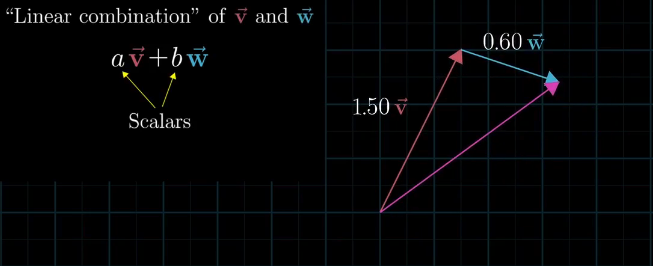
缩放两个向量并使两者相加的操作，称为这两个向量的线性组合。为什么要用“线性”这个词呢？与线有何关系呢？

张成空间

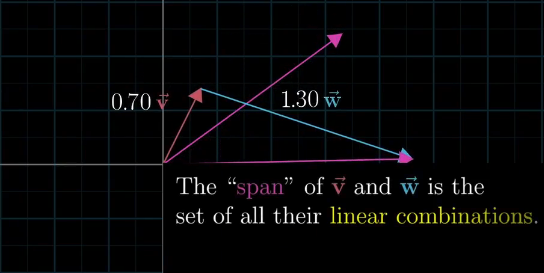
已知一对向量，用其线性组合所获取的所有可能向量的集合，称为这两个向量的张成空间。大多数二维向量对的张成空间包含二维空间的所有向量，如果两个向量共线，则其张成空间包含所有头部落在某一直线上的向量。

向量看做点？

为什么人们经常会把向量看作点？

如果所有的向量都位于二维平面是不是有些拥挤，所以，在处理这类向量集合时，我们通常会用空间里的一个点来表示一个向量，也就是向量头部所在的那个点，和之前一样，我们默认向量的尾部在原点。

总地来说，如果你只研究一个向量，那就把向量想成一个箭头，如果要研究向量集，那就将向量想成点。

线性相关

如果第三个向量落在了前两个向量的张成空间上，或是两个向量共线了，我们有一个术语，可以描述这种至少有一个向量冗余的情况，此时张成空间不会有任何变化，无论什么时候，只要你有多个向量，而且可以在不减少张成空间的情况下删除其中一个向量，那就可以说这些向量是线性相关的。

也就是说，其中一个向量可以用其它向量的线性组合来表示，因为该向量落在了其它向量的张成空间上。

为者常成，行者常至