Python:线性代数-向量-求解简化的方程组 (四十六)

求解简化的方程组

向量与标量的线性组合将延伸出以下这个重要概念： 线性方程组。

在此线性代数课程中，我们将仅深入介绍有两个方程和两个变量的方程组。

在更宽泛的线性代数课程中，你将详细了解 含有n 个线性方程的方程组，其中 n可以是任何数字。

假设有两个变量：

• \(\vec{x}=\begin{bmatrix} -14 \\2 \end{bmatrix} \)

• \(\vec{y}=\begin{bmatrix} 5 \\-1 \end{bmatrix} \)

我们想要将新的变量：\(\begin{bmatrix} -13 \\3 \end{bmatrix} \) 表示为 \(\vec{x}\)和\(\vec{y}\)的线性组合。

换句话说，我们要计算使以下方程成立的两个标量，称之为 a 和 b:

上述方程组称为有两个变量、由两个方程组成的方程组。

可以通过三种理论方法求解该方程组：

- 图形法
- 替代法
- 消元法

下面，我们将详细介绍这三种方法。

图形法

绘出这两条线（线性图）并找到交点。

交点是 (a,b) 的解，因为它是同时位于这两条线上的唯一点。换句话说，它是唯一满足这两个方程的点。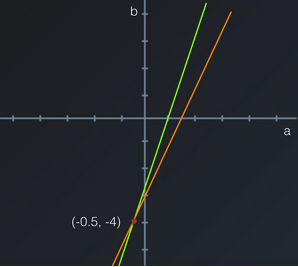

可以清晰地看出：

a = −0.5 和 b = −4

替代法

在其中一个方程中分离出一个变量，然后在第二个方程中替换它

这种方法将使方程组缩减成有一个变量的一个方程。

在我们的示例中：
(1) −14a + 5b = −13
(2) 2a − b = 3

从 (1) 得出 2a − b = 3 ⇒ b = 2a − 3
在方程 (2) 中替换 b
−14a + 5(2a − 3) = −13 并求解 a。

运用简单的代数知识后得出 a = −0.5
替换上述方程 (1) 或 (2) 中的 a，得出 b = −4。

消元法

在此方法中，我们将通过乘以相同的数字，即某个标量（系数）的绝对值，消去其中一个变量。

我们再看看这两个方程：

（注意：两个方程乘以的标量 bbb 即系数 bbb 的绝对值都是 5）。

现在将它们相加。

得出有一个变量的以下单个方程：

−4a + 0b = 2

或者：

−4a = 2 ⇒ a = −0.5

替换任何一个方程中的 a，得出 b = −4。

最终答案：

在此示例中，两个系数均为负数。思考下，如果都是正数或一正一负，该怎么办？

再思考另一个问题：

有两个线性方程和两个变量的方程组始终有解吗？如果有解，始终是唯一解吗？

接下来的几道练习将帮助你回答这个问题。

练习题2

思考以下问题：

有两个线性方程和两个变量的方程组始终有解吗？如果有解，始终是唯一解吗？

看看以下方程组：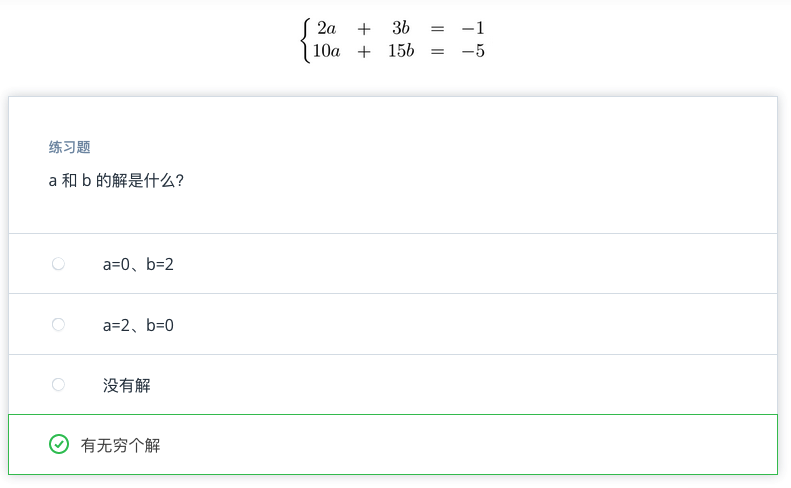

这两个方程是线性相关的。

试着绘出图形。看到什么规律了吗？有多少个交点？

因为这两个方程是线性相关的，因此从图形上来讲，它们定义的是同一条线。因此这个方程组有无数个解。直线上的每个点（用蓝色 x 表示）都满足方程。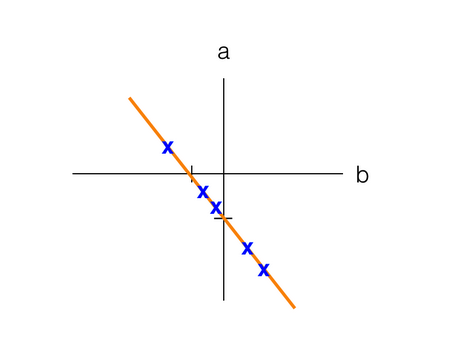

练习题3

看看以下方程组：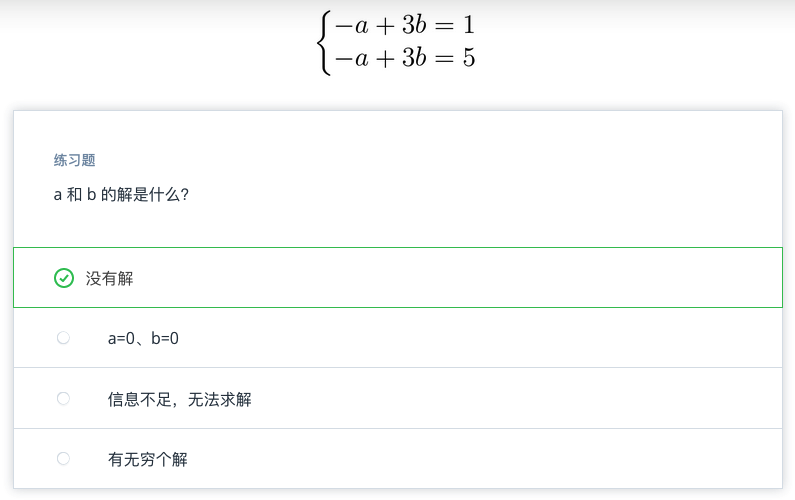

没有解是什么意思？为何会这样？
试着绘出直线，看到什么规律了？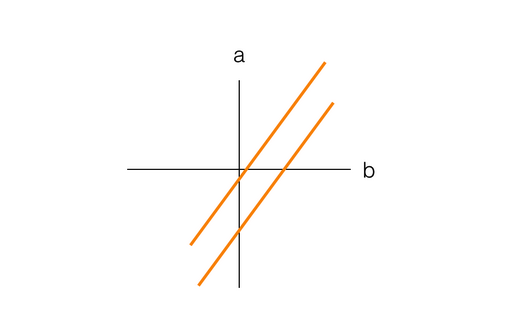

因为这两条直线平行，不相交，因此没有解。（因为图中没有一个点能同时满足这两个方程）。

作为对比，下图中的两条线表示有一个解的两个不相关线性方程。 解是图中同时满足这两个方程的点（用蓝色 x 表示）。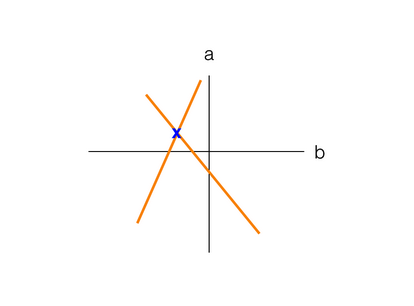

为者常成，行者常至