Python:线性代数-矩阵-算法-加法和乘法 (四十八)

矩阵加法

要将一个矩阵与另一个矩阵相加，我们需要：

• 验证确保两个矩阵的维度相同
• 按照相应的正确索引将元素相加

我们通过一个示例来理解这方面的要求：
我们将侧重于在 方程 11 中看到的随机矩阵：

矩阵 A 的维度为 mxn。 这意味着该矩阵具有 m 行和 n 列。

矩阵 A 只能与另一个具有 m 行和 n 列的矩阵相加。例如矩阵 B。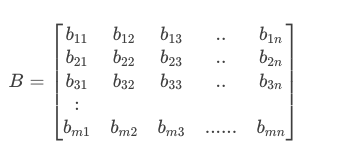

只要维度相同，加法就很简单：

只需将 A 中的元素 \(a_{ij}\) 与 B中的相应元素 \(b_{ij} \)相加即可。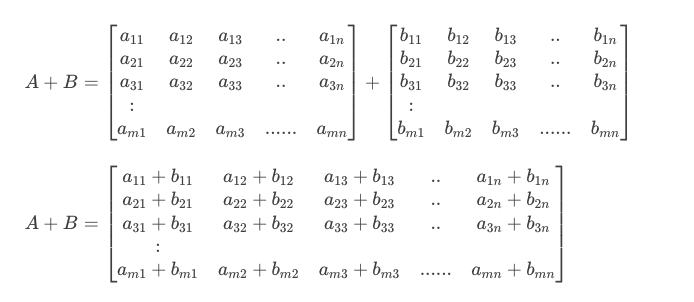

矩阵的标量乘法

要将矩阵与标量相乘，我们不需要验证维度或指数。

只需将矩阵中的每个元素与标量相乘即可！

例如：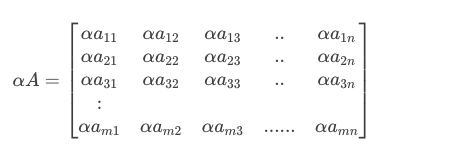

练习

对于以下情形，矩阵 D 的第 ij 个元素的值是多少？

方形矩阵的乘法

将两个矩阵相乘时，我们需要考虑每个矩阵的维度，如果维度不能合理匹配，则无法相乘。
最简单的乘法是两个具有相同维度 nxn 的*方形矩阵相乘。

方形矩阵是行数和列数相同的矩阵。

下面是一个 mxm 方形矩阵。它有 m 行和 m 列。

上图矩阵 A 可以与其他维度相同的矩阵 mxm 相乘。

结果是一个维度相同的新方形矩阵。

演示实际乘法过程的最简单方式是看一个示例：

假设 P 和 Q 是两个 3x3 方形矩阵。

注意在乘法结果中查找每个元素的规律。

PxQ 中的每个元素 ij 是将矩阵 P 的行 i 中的所有元素与矩阵 Q 的列 j 中的相应 j 元素相乘的结果。

请看下图：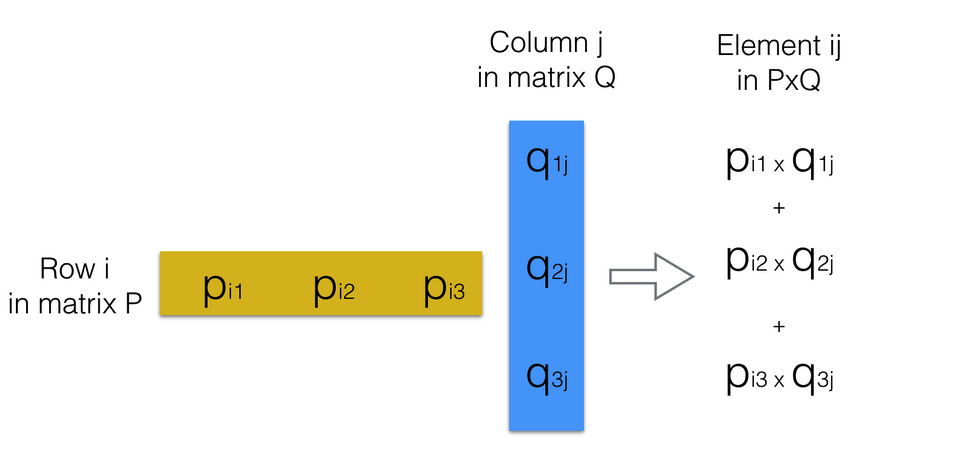

如果 A 是一个 n × m 矩阵，B 是一个 m × p 矩阵，它们的矩阵积 AB 是一个 n × p 矩阵，其中 A 的行上的 m 个元素与 B 的列上的 m 个元素相乘，得出矩阵积 AB。如果用矩阵表示两个线性变换，则矩阵积表示两个变换的合成结果。

方形矩阵乘法练习

假设 A 和 B 是两个 3 x 3 方形矩阵。

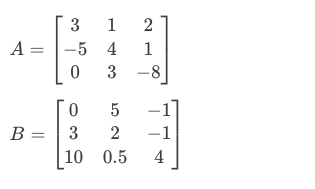
(a) 矩阵 C 的元素 \(c_{23}\) 的值是多少，其中 C=A x B
(b) 矩阵 C 的元素 \(c_{23}\) 的值是多少，其中 C=B x A

注意 A x B ≠ B x A，因为 A x B 中的元素 \(c_{23}\) 与 B x A 中的元素 \(c_{23}\) 不同。

因为 A x B ≠ B x A，我们称之为不满足交换律。这是一个有趣的现象，标量乘法肯定是满足交换律的。

矩阵乘法

到目前为止，我们仅讲解了方形矩阵乘法。但是，矩阵乘法不限于方形矩阵乘法。

我们再来看看表示乘法 P x Q 的图形：

注意，这里的顺序很重要，因为矩阵乘法是不满足交换律的。

如果你仔细观察表示乘法 P x Q 的图形，你将发现 P 中的列数等于 Q 中的行数。（在我们的示例中，数量为 3）。

矩阵 P 中的行数是多少？矩阵 Q 中的列数是多少？这两个数字决定了乘法结果的维数。

换句话说，如果 P 是一个维度为 t x m 的矩阵，Q 是一个维度为 m x v 的矩阵，那么：

• PxQ 是可行的，因为维度匹配。（P 有 m 列，Q 有 m 行）。
• PxQ 将是一个 txv矩阵。（有 t 行和 v 列）。

我们来看一个示例：

我们想要计算 PxQ。

第一步是检查计算是否可行。我们将查看矩阵的维度。

矩阵 P 有 3 列，矩阵 Q 有 3 行。很棒！可以相乘。

相乘的结果 PxQ 维度为 2x4（有 2 行和 4 列）。

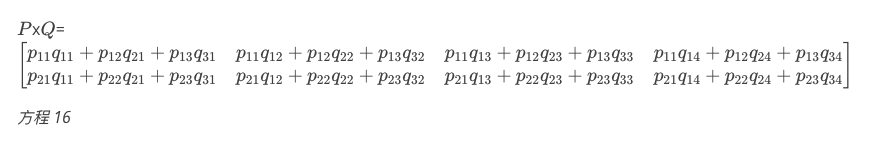
矩阵乘法练习

假设 A 是一个 1 x 5 矩阵，BBB 是一个 5 x 3 矩阵。

注意 A 实际上是一个行向量！只有一行或一列的矩阵是一个向量

• 只有一行的矩阵是行向量
• 只有一列的矩阵是列向量

C = AxB ?

为者常成，行者常至