Python:线性代数-矩阵-线性变换和矩阵 (四十九)

线性变换和矩阵

线性变换必须满足两个条件：

• 1、位置必须在原点
• 2、必须是直线

我们只需要四个数字，就能描述一个二维线性变换，这四个数字就是 \(\vec{i}\) 变换后的两个坐标和 \(\vec{j}\) 变换后的两个坐标，通常我们会把这些坐标打包放在一起。

矩阵的列就是两个向量\(\vec{i}\) 和 \(\vec{j}\) 变换后的位置，如果给你一个描述线性变换的二乘二矩阵和某个具体向量，求线性变换后的向量，你就可以分别将向量坐标与相应的矩阵列相乘，再进行相加，结果就出来了。这与将经过缩放的新基向量相加本质上是一致的。

请牢记：第一列的值 a 和 c 是第一个基向量移动后的坐标，第二列的值 b 和 d 是第二个基向量移动后的坐标，对某个向量[x, y]进行这个变换

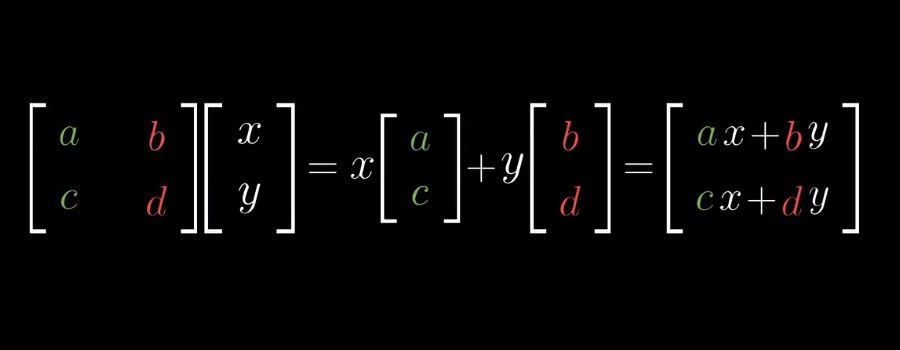
根据矩阵来推导变换公式：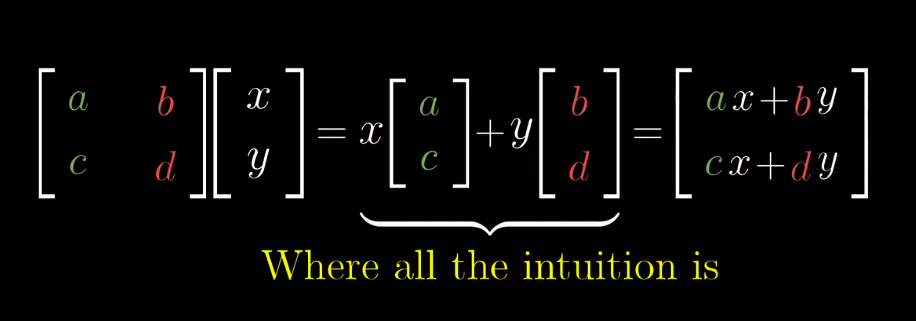

看到一个矩阵，你就可以将其看作某种空间变换，一旦你彻底理解了这个思路，你就能深刻地理解线性代数了。

为者常成，行者常至